前哨站中部装甲板击打策略

猜测

前哨站底部小装甲改为旋转式小装甲，现在旋转方式不明。估计应该和小陀螺^1差不多，且应该不会太快。

所以我认为前哨站底部小装甲应该是一个缓慢旋转的小陀螺，但击打策略应该与小陀螺不同，有以下几点。

前哨站装甲板旋转应该不会像小陀螺这么快，所以正常小陀螺时旋转速度大于识别速度的情况应该不存在，故可以进行一定的预测击打
击打小陀螺仅需判断出车的位置，瞄准车的中心点击打即可。但前哨站特别是英雄机器人在击打时应该目标是能够准确击打到小陀螺的位置。因此需要准确判断装甲板的位置。

前哨站介绍

前哨站的机制已经更新，由下图可以看出，前哨站中间偏上总共有三块装甲板，装甲板呈中心对称。旋转半径约300mm。

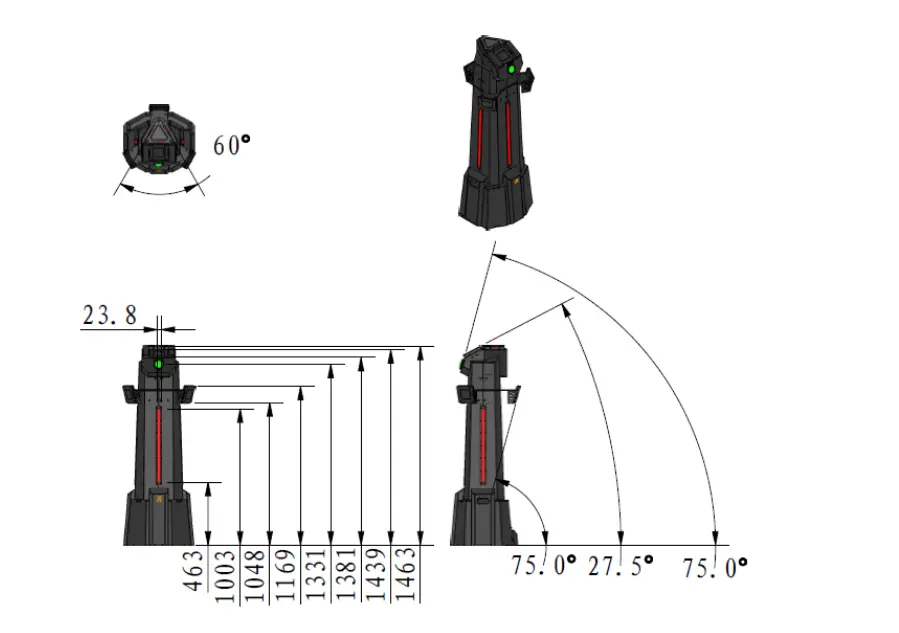
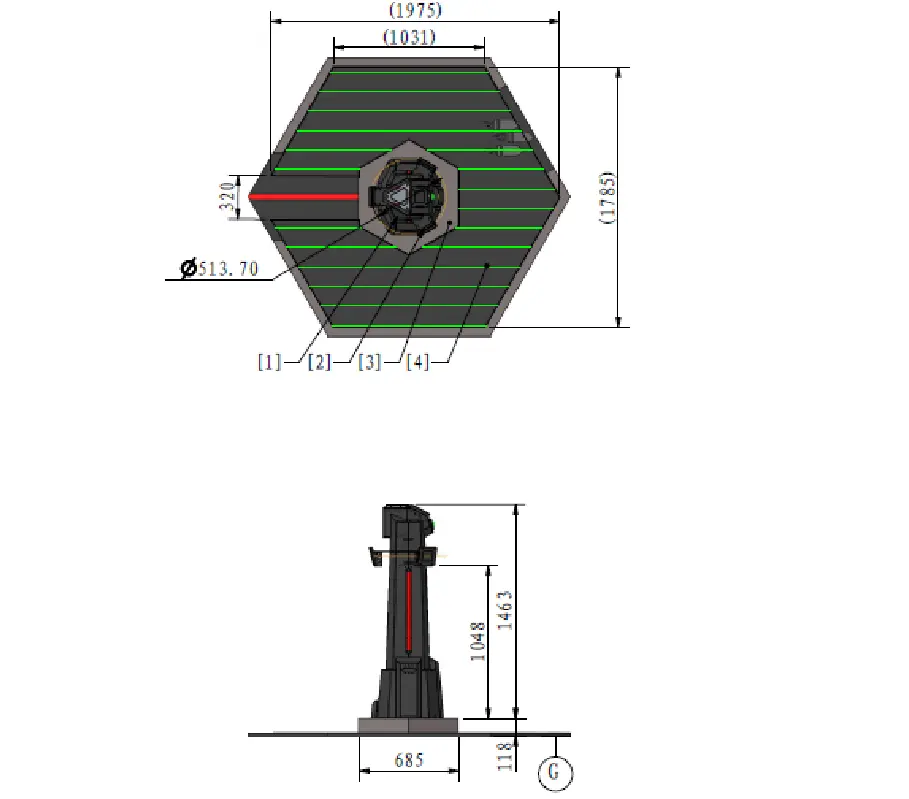
前哨站的旋转机制

模拟结果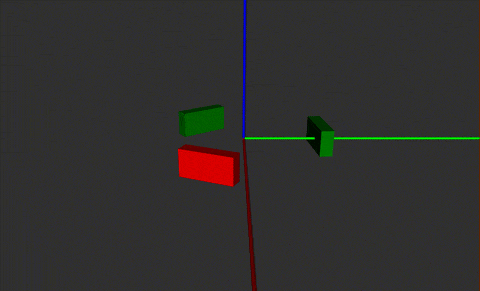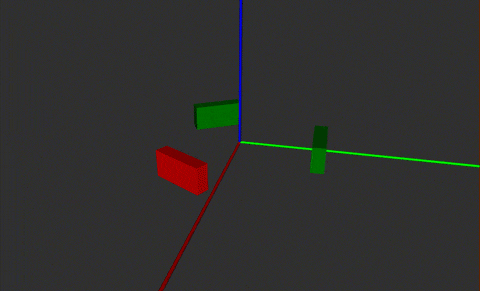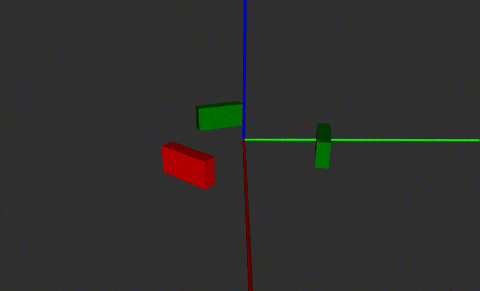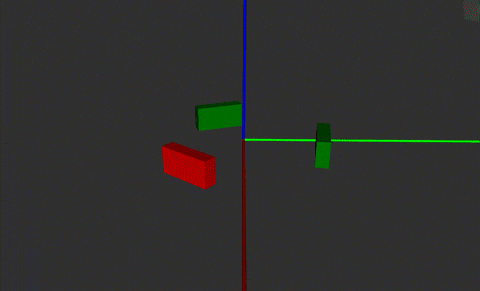

以下为官方文档：

慢速小陀螺状态

翻了一下之前视频竟然还真有一个光原地旋转而不是小陀螺的视频(云台一起转)，转的比较慢，应该和前哨站下装甲板差不多，缺点就是旋转半径和前哨站区比较小。

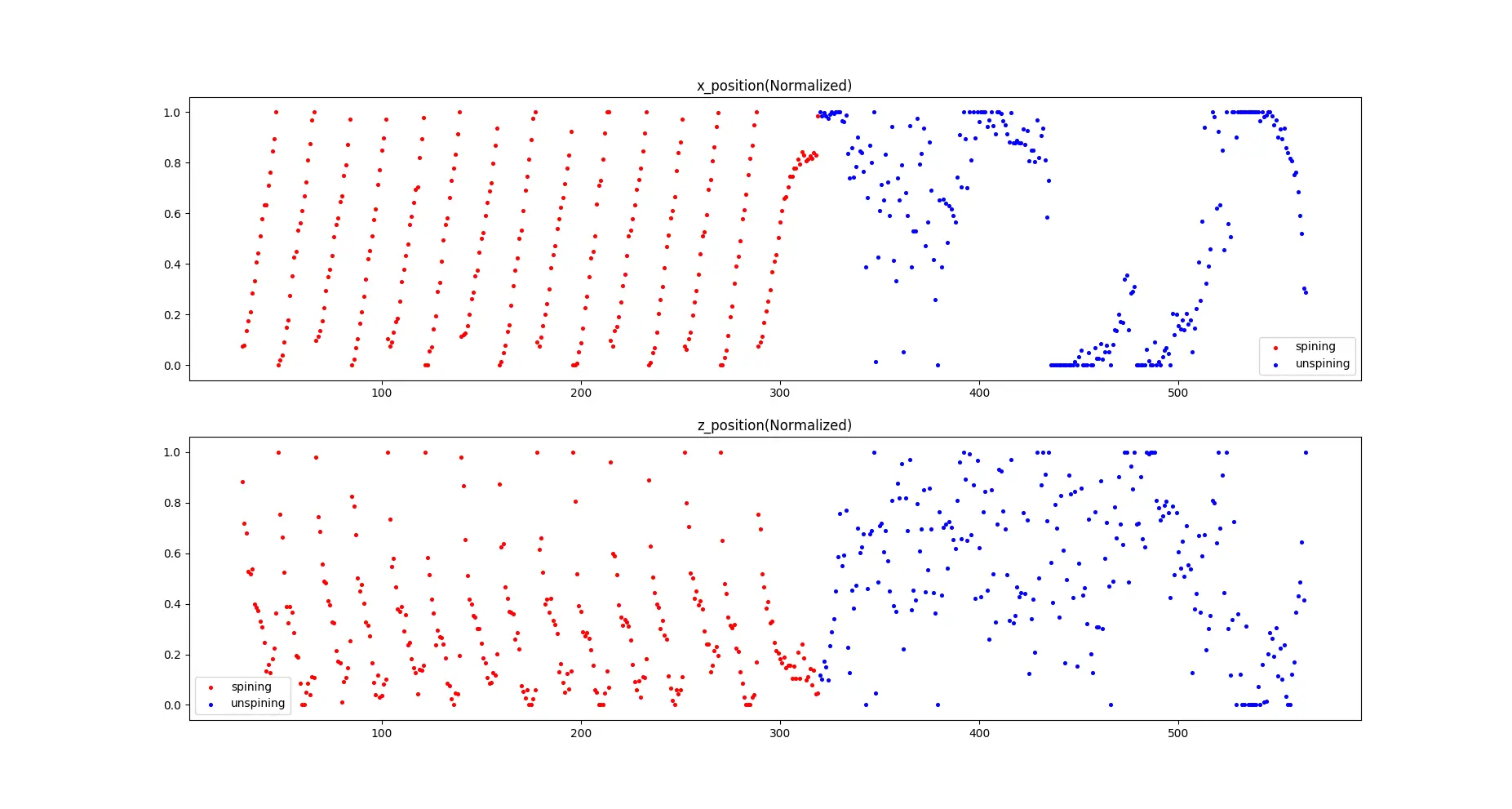
时域

其旋转状态下主要为x坐标和z坐标发生变化，如下图

频域

可以看出x的变化还是非常的明显的，可以以此为依据判断陀螺状态，问题就是怎么让计算机理解它处于陀螺状态。本以为变换到频域之后会很明显，结果fft之后效果并不是特别好。

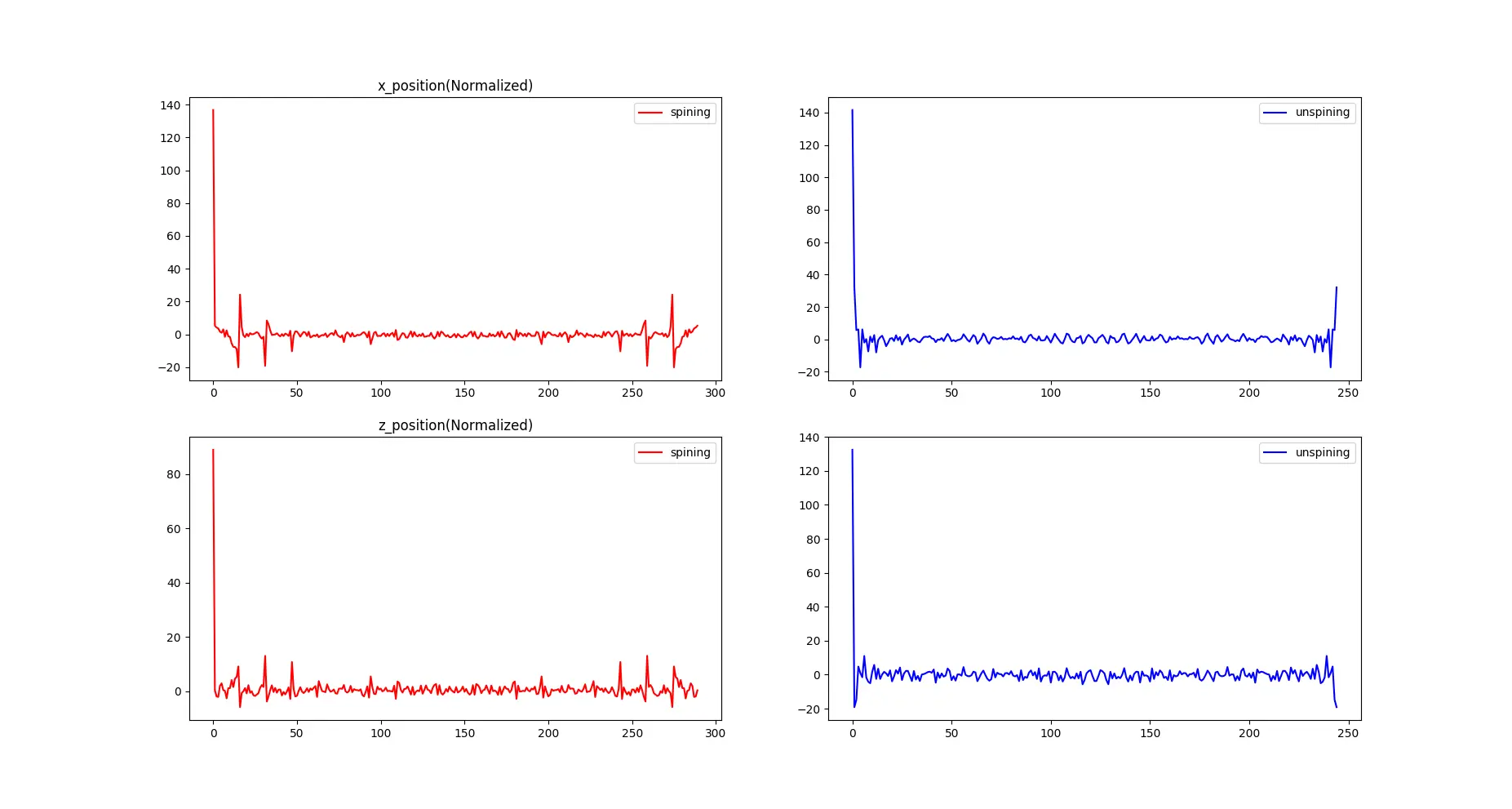
上图中左图为陀螺下的x和z的频域变换，而右图为随意运动下的频域变化，似乎不是太明显。

一阶差分

对位置进行一阶差分后进行观察，可以看出会存在一些离群点是因为装甲板的迅速切换。但是考虑到实际中可能每次装甲板切换(不一定是小陀螺)都会产生这种东西，依然不是太好判别

旋转模式的判断

要判断是否处于陀螺模式，经过上述研究，最终还是决定直接从时域上进行观察，还是时域上特征最为明显。

在时域上，最为明显的特点是不断增加然后突然返回原来的值然后又重新开始向上增加，针对这个特点需要设计一套算法。

算法放置位置

反陀螺模块可以放在决策前，也一放在决策后。

放在决策前：需要同时对多个装甲板进行判断，但考虑到传统逻辑时间复杂度不高，时间复杂度上的影响可忽略不计。可以通过不同的数字来对装甲板进行分类，唯一的问题是写起来会比较麻烦，同时需要与决策相结合。
放在决策后：仅需要对决策出的最优装甲板进行判断，比较简单，初代版本先考虑此。

神经网络

首先先无脑上神经网络看一下效果怎么样。针对这种时间序列数据，先试一下比较有名的长短神经网络lstm。原理在此不赘述，但现在由于数据集不足的原因，先不用这种无脑不优雅的方法

传统逻辑

为了简化问题，我们首先假设该旋转物体的坐标不变，即原地旋转，这是针对小陀螺的情况。

通过观察前面时域上的特点，我们总结出一下几个规律：

坐标变换呈现周期性，每个周期有一次跳变，这个跳变代表了切换装甲板的过程。设相邻跳变间的时间间隔为$T_0$,假设车辆有四个装甲板，则目标旋转一圈的周期为$T=4T_0$,角速度为$\omega=\frac{2\pi}{T} = \frac{\pi}{2T_0}$
每次跳变之后坐标变化均单调且方向一致，可近似为线性

基于此我们给出检测逻辑：

首先同一目标的数字必然相等，因此需要进行众数滤波，将不属于该车辆的数字剔除。
然后对所取序列进行判断，预计需要看到目标旋转一圈，所以先取$N = 100$帧，进行归一化,（由于不知道敌方前哨站转速，对于前哨站可能100帧不太够）
检测跳变点，即首先做对所取序列做一阶差分，取出绝对值较大的点,跳变点的跳变距离需要比较一致。
判断周期性，即判断相邻跳变点之间相邻点数是否相似，或者时间间隔是否相似
判断单调性，即相邻跳变点之间的点是否单调且方向是否相同。具体方法为，取两跳变点之间的序列，从前向后依次判断，设一个值cnt，若是前大于后则+1，否则-1，判断其绝对值是否大于阈值$Mon$,$Mon$为两跳变点之间的序列长度乘0.75

静态陀螺

反旋转中最简单的便是敌方车辆原地旋转的时候，此时的击打策略为：

击打敌方车辆中心点。原因在于由于车辆的原地小陀螺确实速度会很快。甚至超过了识别和子弹滞空时间^2，所以没办法进行预测，就算预测也效率不高。
取敌方车辆中心点的方法为：取每一个周期的平均值即可。

动态陀螺

动态陀螺同样是击打目标中心点，与静态陀螺唯一的区别就是：

动态陀螺需要取最近一个周期的平均值

前哨站下装甲击打

前哨站下装甲击打比较独特，与反陀螺模式不同，原因在于：

反陀螺主要是我方步兵或者哨兵击打对面步兵或英雄。小陀螺转速较高，射频较高，可以浪费一定子弹，不追求百发百中。所以只需要瞄着对面车辆中心点打即可。
前哨站下装甲板击打由我方英雄击打敌方前哨站。前哨站转速较低(估计),英雄射频较低，子弹宝贵，追求百发百中。必须预测出装甲板出现的位置，可能类似击打能量机关，但远比击打能量机关简单。

现在已知前哨站的装甲板是以0.4r/s的速度旋转，旋转半径约300mm，一共有3块装甲板，

策略一

为了简化问题，首先假设旋转模式下x轴的运动为线性运动(实际上为余弦运动)。思路是：

由于前哨站装甲板有唯一数字，不需要经过旋转判断，但是可以通过旋转判断改进从而知道其旋转周期$T$,以及角速度$\omega$，至少旋转经过一次跳变才能知道
然后需要确定其预测时间$t_p$，这个时间由目标装甲板的距离和弹速唯一确定。
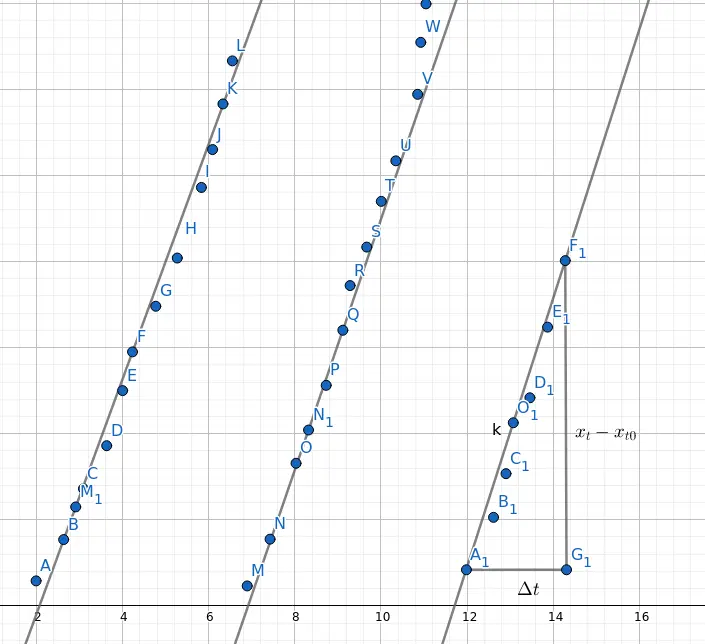
判断其当前所处相位，有一个比较简单的方法是。先判断跳变点之间的单调递增的函数，由于跳变点之间都是单调递增的，可以通过最高低点之间的值简单判断其斜率$k$。然后带入当前点值$x_t$减跳变点值$x_{t0}$再与斜率$k$相除即可得到相应时间

$$
k=\frac{x_{top} - x_{bottom}}{t_{top} - t_{bottom}}=\frac{x_{top} - x_{bottom}}{T/3}
$$

其中$x_{top}$和$x_{bottom}$为之前的最高点和最低(顺便验证k值计算的准确性)
$$
\Delta t = t-t_0=\frac{x_t - x_{t0}}{k}
$$

(其中$F_1$为当前点)

此时分为两种情况即
- $\Delta t +t_p < T$ 时，预测的坐标为$x_p = x_{t0} + kt_p$
- $\Delta t +t_p \ge T$ 时，预测的坐标为$x_p = x_{t0} + kt_p -(x_{top} - x_{bottom})$

存在的问题

经过仿真之后发现，装甲板的旋转得到的数据曲线并非如上图所示，因为只有三个装甲板，每个装甲板间隔120°，也就意为着每隔一段时间必有一部分时间无法识别到装甲板，所以中间应该是有间隔的。
无法确定装甲板转到什么角度可以识别到，且事实上也存在着一定的随机性。
预测精度受采样率干扰很大。
上述将运动简化为线性运动存在一定的问题。实际上他是一个正弦运动
当画面中正好转到装甲板识别不到的画面时无法预测

策略二

时间计算：
首先进行一些简单的时间计算我们可以得到。已知装甲板的角速度为0.4r/s，即装甲板每秒旋转0.4圈。而由车辆小陀螺我们可以得到，装甲板可以被识别的窗口期至少有0.25圈，那么也就是说每个装甲板每次可以被识别到的时间为625ms，假设每次自瞄时间8ms，则每次装甲板识别周期共计可获得约78个采样点。这么一想，感觉还是蛮多的。

通过上面的时间计算，对于这种采样点较多的情况可以采用这种方法。但实际上，还有一个非常简单但却十分实用的方法，我称之为时间回溯法，很简单。

首先采样大概装甲板转过半圈的时间，大概1s多。注意，采样时需要采样装甲板坐标x的值以及对应的时间戳t。用一个数组存起来，大概150个采样点。
现在正式预测。由于已知旋转一圈的周期为2.5s，一共三个装甲板，即每个装甲板识别周期就是2.5/3=0.833s=833ms。那只需要看(833ms-需要预测的时间tp)前那时的x坐标即为预测的坐标

这种方法十分粗暴却有效，当然前提是已知旋转的周期。
下图为仿真的结果：

别看这方法简单，但我认为这是可行性最高的方案，原因在于：

经过时间计算发现采样点数量足够
可以在未识别到装甲板的时候进行预测
方法简单就是它的优点

仔细一想没有太大的硬伤，越想越妙。简单有效。唯一需要调的参数为预测时间，即为以下的时间相加：

视觉识别的时间(8ms左右)
通讯时间(0.5ms左右)
电控处理时间
控制时间
子弹滞空时间(关键影响)

并且